Accessible Mathematics: Ten Instructional Shifts That Raise Student Achievement - Summary Notes

🚀 Summary of the Book in Three Points

1. Show different representations of the same concept you're teaching, not everyone thinks or visualizes Math the same way you do; therefore, pictures, graphs, tables and many more things can be used to supplement the abstract mathematical signs and symbols already on your board.
2. Always have students justify their answers, whether they're right or wrong, because the point is to encourage them to think through their thought process rather than to jump to the answer and hear only a "correct" or "wrong" from the teacher.
3. Use skills used in literacy classes for Math, make them think through their answers, make predictions, inferences, formulate sentences and make sure the sentences are precise. Last but not least, make sure the classroom is Math language-rich, constantly bringing up newly learning words in newer and newer contexts. More often than not, difficulties in Mathematics are language-related rather than arithmetic-based.

🙋🏽‍♂️ Who should read it?

This book is great for both Math and non-Math teachers alike, and all people who have some sort of "teaching" role in any aspects of their lives. While the book constantly refers to mathematical terms, it's more focused on the delivery of the lesson than the subject of Math itself, and that lends this book to be one that can be used in a transdisciplinary manner.

🔍 How I discovered it

I discovered this book through a personal development seminar in which the book's author assigned me to read this book.

☘️ How it changed me

While it changed me as Math teacher, it also changed me as a general educator. When someone doesn't understand your point, you should find different ways to represent those points to better close the gap between the teaching and learning gap

Notes

Try to move beyond having the "one right answer", and focus more on the reasoning process

• When we learn addition, we learn to add by saying 9+9 is just counting up 9 more to get 18. But you can also reason that 9+9 is equal to (9+1) +(9-1) or in simpler terms, take away 1 from one of the nines and give it to the other 9 to make it a simple looking 10, to make life easier when adding.

Small choices don't make much of a difference at the time, but add up over the long-term.

• Broaden the scope of a lesson by reviewing past concepts cumulatively for the first few minutes, as small skill reinforcements add up to a significant retention of those skills long term.
• This ties into a lot of habit building concepts mentioned in James Clear's Atomic Habits book, small changes happen when done with enough repetition.

Show more, tell less

• When you can, try to talk less and show a picture of the concept you're talking about more. Visualize things and go beyond merely using math symbols and words.

Set evidence that proves to anyone that students have accomplished the lesson objective

• Lessons should be planned with both the students and teachers knowing what targets are trying to be met. This means you'll need to have learning goals written somewhere on your presentation, and an exit ticket so that students have feedback on what they retained on the culmination of the lesson. The whole class needs a clear sense of where this Math train is going!

Not every visualization works for every student

• While some students can memorize rules for fractions other students need a visual representation of it. They need to see how a quarter is one piece out of 4 total pieces that make up a whole, and mere letters and words don't show that.

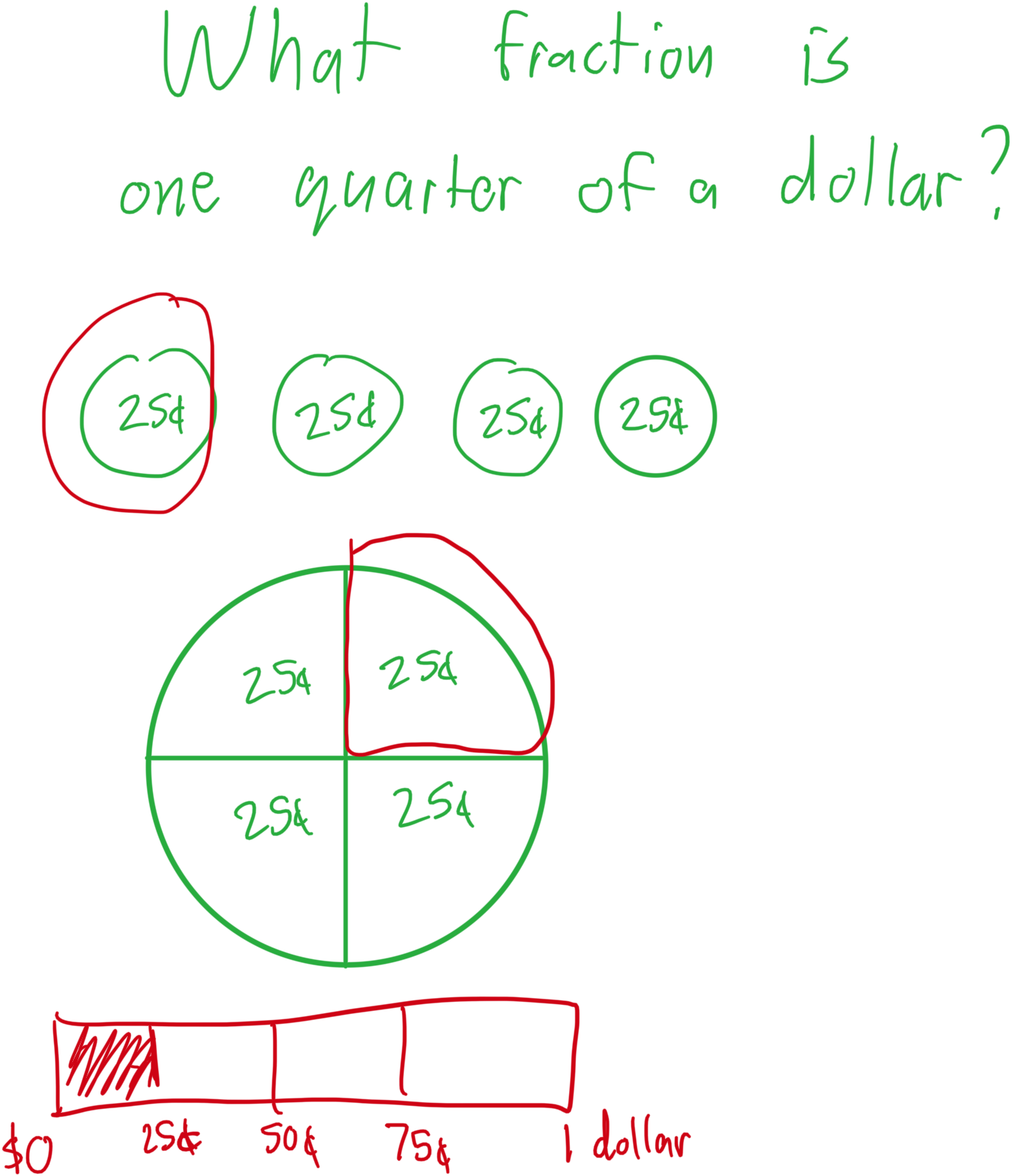
• Visual representation of an answer is another way to see if students understand how a real world application of a value should look like. If student fails to show it properly, it can show a gap in knowledge.

Explanations provide invaluable opportunity for students to clarify their reasoning and use mathematical terms

• Similar to early on where I mentioned the two ways to add 9+9, students may come up with even more intuitive algorithms that work for them, and it is our job to celebrate those differences in reasoning so long as they clarify their reasoning using the necessary academic terms.

When a student answers something, use "why" as an alternative to "yes" or "no" so that the student doesn't feel dumb for being wrong, and an atmosphere of "even the correct answer needs a justification" is brought in the classroom

• Justifying your answer is more important than the answer itself as it reveals any holes in a student's knowledge.
• Follow-up a student's answer with a question about their thought process rather than just "good job"
• One way to improve arithmetic is to give the equation with the answer and then ask students to convince you that it's true.
• Conversely, you can also ask why it's not true.

Use cumulative review every day as a mini-warm up, and put in variations in how you present it to the students and how they present their understanding back to you to promote student engagement

An immediate focus on Math can be placed as a provocation, as soon as the students walk in the classroom, settle in, and get out a mini-whiteboard or notebook to attempt a series of weird and engaging math questions they see on the whiteboard:

"Good afternoon students!
Today's numbers are one to six."
What is 6 times 7?
What number is 2,000 less than 18,294?
About how much is 29 cents and 34 cents?
What is one tenth of 500?
Draw a picture of 3/4.
Estimate my weight in pounds.

This type of review will happen daily but with different variations of questions. Daily cumulative review is one of the plethora of ways to extend the scope of a single lesson beyond just that day’s major objective. You can also think about it this way:

Five to eight minutes each day for review, times 180 days, is fifteen hours! That’s about half a college course, or half an hour a week of tutoring for an entire semester.

Again, we encounter the theme of small daily changes lead to big results over time!

Students can analyze data in two ways - 1 milk the data by asking questions about it - 2 form answers from the data and see what questions the answers are answering

• This prepares students to not only make sense of data, but to draw conclusions from it and reinforce the skill of forming and answering questions about data sets.
• Steer students away from focusing on the right answer by explicitly instructing them to form their own questions and answers

Start with a familiar context, lead to open-ended questions, then talking with peers, and be enthusiastic along the way

• Use the Guinness Book of World Records, something that is popular amongst children, and add an element of your lesson to it. They are more likely to take ownership over their learning, ask their own questions and debate with their peers about whether their math is reasonable when they have a strong attachment to what is being presented.

Simply telling someone how to do something is a short term success

It does not guarantee that they'll be able to reintroduce the same method in new contexts.

Script your instructional questions so you don't forget to ask students

Expect some common pitfalls when teaching a specific skill. This also means predicting any questions students may raise and answering them in a timely fashion.

Reviewing before the beginning of a new lesson before learning a new skillset hones your overall skillsets, reinforces essential pieces of knowledge that need to be maintained, and allows for pre-diagnoses for gaps in knowledge

• This provides opportunity for a pre-diagnosis.
• You can reinforce skills needed throughout the year. For example, definitions, estimations, facts of numbers, and more.

Reverse engineer given answers to work out problem solving strategies

3.14, 3, 6

Students could probably take a look at these three numbers and start to assume it's about some circle. They can come up with a way to solve some imagined problem, like "what is the circumference of a circle with a diameter that is 6".

This is also my favourite strategy of testing students, as it doesn't go to to the answer, but works its way backward to knowing how to make the question.

Reflect on each lesson to perfect the lesson next time you teach it

If you've ever had these thoughts,

If only I did this and this at 20 minutes into the lesson

Then you're in luck! You are always going to experiment with your teaching style but you need to document what works and what doesn't and practice putting that into practice. Rinse and repeat!

Keep in mind reminders about vocabulary, connections to other things, common mistakes and misconceptions BEFORE and DURING the lesson

Justifying reasons or proposing alternative solutions raises cognitive demand and what the student should value in the solving process than merely just giving an answer

The kinds of questions that support instruction like this include
- Is that reasonable? How do you know?
- Why do we know the answer must be less than ten?
- How do you know that it can’t be negative?
- What makes that a rectangle?
- What assumptions are you making?
- “Why?”
- or “How do you know?”
- or “Can you explain your thinking?”
- “Is that reasonable?” or
- “Convince me that one tenth of 680 is 68?”

Distributed practice and ongoing cumulative review is the most effective way to learn a skill that will stick

• Strongly supported by research. Distributed practice is synonymous to "spaced-repetition" which has mountains of evidence supporting that it works.
• It is also evident in classroom observations.
• In most classrooms, it's not common
  • Warm-ups are target at skill or concept of day and not past stuff... oh no!
  • homework focuses on the content given that day and doesn't incorproate previous concepts ... oh no! We don't want to practice one skill one time and forget about it forever!

Asks students whether it is not [the right answer] without saying it is the right answer, and note whoever raises their hand

Take this situation for example

“Class! Raise your hand if the answer to number one is not 42.” This question quickly shows you how many of your students may still be struggling with this troublesome multiplication fact and provides positive reinforcement for the progress the class is making.

Goodreads Review:

Accessible Mathematics: Ten Instructional Shifts That Raise Student Achievement by Steven J. Leinwand
My rating: 5 of 5 stars

Some great points he made

1) Use things that work in reading literacy classes to improve mathematical literacy. Prediction, inferences, the whole shebang. This is especially true as students try to solve word problems that are multi-factorial in the dimensions of thinking that are needed.

2) Use multiple representations of the same thing! A quarter can be represented by a pie chart, 25 cents, or a piece of 4 whole pieces. Do more to show that what you're talking about is not mere numbers and symbols on a chalkboard.

3) Distributed cumulative practice is proven to work better for skill retention. In layman's terms spaced repetition but incorporating all knowledge learned thusfar and not just the skill at hand is king. Always take the opportunity to bring back concepts from older lessons in your warm-ups.

4) Have students justify and criticize math where possible. Math is a special case of philosophy where argumentation is often about the numerical nature of the world and it has room for things philosophers often enjoy doing because of it, debating!

See full review: https://www.soroushtorkian.com/access...

View all my reviews